Connect Four - Deep Reinforcement Learning
I recently stumbled uppon the amazing Connect Kaggle Competition and I tried to improve my humble knowledge on reinforcement learning by participating in this challenge.
The task
Very simple: Write an agent that plays
Connect Four against competing algorithms.
My way to tackle it: “Deep” Q-Learning
Sure, I could write some deterministic code on how to proceed in the game but what I actually implement is a seemingly brute-force method: Let the agent play the game over and over again and learn the rules the hard way. More specifically, the agents receives information on the current observation (the current state of the board) and then has to take an action (which slot to choose to add a coin). After that, nature responses with a new state and potentially yields a reward (if the game is won) or a penalty (if the game is lost or if the agent chooses an action that is not valid - such as putting a coin into an already full slot).
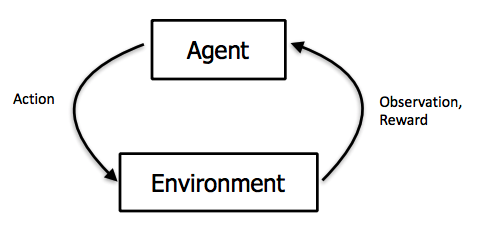
How should the agent decide on her action? In finance, the concept of dynamic programming, more specifically, the Bellman-equation, is well-known: Aim at actions that yield the highest expected reward. You can do so, by value each (action, state) pair with respect to the immediate rewards and the transition into the next_state. More specifically, you value an action $a$ given the current state $s_t$ as
$$Q(a, s_t) = r + \gamma\max\limits_{a’}\hat{Q}(a’, s_{t+1})$$
where $\gamma$ is a discount factor and $\hat{Q}$ is the (predicted) value of the next state. If we’d play a simpler game, we could try to store all possible (action, state) pairs and compute the optimal action. However, Connect Four in its basic fashion has 4531985219092 different possible states, so good luck with that aproach (which would be called Q-Learning, by the way).
What I do instead, is approximating this function using a Neural network, simply because I have always wanted to implement something like this. The python kernel below summarises my implementation and tremendously benefits from Hieu Phungs work on Q-Learning and Keon Kims blog.
Initialization
Below packages are setting up the environment. Kaggle provides an entire framework to test your agent. keras is using the TensorFlow backend to handle the neural network.
import gym
import numpy as np
from math import exp, log
#import random
from random import choice, uniform
from collections import deque
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from kaggle_environments import evaluate, make
Using TensorFlow backend.
Define Environment
The ConnectX environment below allows to play around with the setup in a clean ‘gym’ style which makes it very easy to interact with current states. In order to train my agent properly, the switch_side and switch_trainer functions are called whenever we start a new game. Therefore, the agent (hopefully) learns to play on both sides of the board against the provided negamax and the random opponent (random just drops coins into arbitrarily chosen slots). For the purpose of illustrating the code, I switch the negamax function of, however.
class ConnectX(gym.Env):
def __init__(self, switch_prob=0.5):
self.env = make('connectx', debug=True)
self.pair = [None, 'random']
self.trainer = self.env.train(self.pair)
self.switch_prob = switch_prob
config = self.env.configuration
self.action_space = gym.spaces.Discrete(config.columns)
self.observation_space = gym.spaces.Box(low=0, high=2, shape=(config.rows,config.columns,1), dtype=np.int)
def switch_side(self):
self.pair = self.pair[::-1]
self.trainer = self.env.train(self.pair)
def switch_trainer(self):
current_trainer_random = 'random' in self.pair
if current_trainer_random:
self.pair = [None, 'negamax']
else:
self.pair = [None, 'random']
self.trainer = self.env.train(self.pair)
def step(self, action):
return self.trainer.step(action)
def reset(self):
if random.uniform(0, 1) < self.switch_prob: # switch side
self.switch_side()
#if random.uniform(0, 1) < self.switch_prob: # switch trainer
# self.switch_trainer()
return self.trainer.reset()
Deep Learning Agent
I am really not an expert in neural nets. Thus, all I do is playing around a bit. The magic in defining the agent as below is happening in the replay function: After gathering some experience, a neural network is trained to make sense of the state, action and reward relationship. The target is set such that the network aims at minimizing the loss between predicting the reward of the next_state and the realized reward.
# Deep Q-learning Agent
class DQNAgent:
def __init__(self, state_size, action_size, episodes):
self.state_size = state_size
self.action_size = action_size
self.memory = deque(maxlen=500)
self.gamma = 0.9 # discount rate
self.epsilon = 0.10 # initial exploration rate
self.epsilon_min = 0.01
self.epsilon_decay = exp((log(self.epsilon_min) - log(self.epsilon))/(0.8*episodes)) # reaches epsilon_min after 80% of iterations
self.model = self._build_model()
def _build_model(self):
# Neural Net for Deep-Q learning Model
model = Sequential()
model.add(Dense(20, input_dim=self.state_size, activation='relu'))
model.add(Dense(50, activation='relu'))
model.add(Dense(self.action_size, activation='linear'))
model.compile(loss='mse',
optimizer=Adam(lr = 0.00001))
return model
def memorize(self, state, action, reward, next_state, done):
self.memory.append((state, action, reward, next_state, done))
def act(self, state):
if np.random.rand() <= self.epsilon: # Exploration
return choice([c for c in range(self.action_size) if state[:,c] == 0])
#when exploring, I allow for "wrong" moves to give the agent a chance
#to experience the penalty of choosing full columns
#return choice([c for c in range(self.action_size)])
act_values = self.model.predict(state) # Exploitation
action = np.argmax(act_values[0])
return action
def replay(self, batch_size):
minibatch = random.sample(self.memory, batch_size)
for state, action, reward, next_state, done in minibatch:
target = reward
if not done:
target = reward + self.gamma * np.amax(self.model.predict(next_state)[0])
target_f = self.model.predict(state)
target_f[0][action] = target
self.model.fit(state, target_f, epochs=1, verbose=0)
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
def load(self, name):
self.model.load_weights(name)
def save(self, name):
self.model.save_weights(name)
Train the agent
Training is nothing as iteratively playing against the trainer, memorizing what happened and updating the neural net weights after each iteration. Notable thing here is that I let the agent also learn what a valid move is the hard way (a move is invalid if the agent chooses a column which is already full). After an invalid move the game is over (done = True) and I penalize invalid actions hard.
# initialize gym environment and the agent
env = ConnectX(switch_prob = 0.5)
state_size = env.observation_space.shape[1]*env.observation_space.shape[0]
action_size = env.observation_space.shape[1]
episodes = 40000
agent = DQNAgent(state_size, action_size, episodes)
agent.load("./connectX-weights_deep.h5") # load prelearned weights
batch_size = 40 # Don't know if this number makes sense
# Monitoring devices
all_total_rewards = np.empty(episodes)
all_avg_rewards = np.empty(episodes)
# Iterate the game
for e in range(episodes):
# reset state in the beginning of each game
done = False
state = env.reset()
total_rewards = 0
while not done:
# Decide action
action = int(agent.act(np.array([state.board])))
next_state, reward, done, _ = env.step(action)
if not done:
reward = 0.0/42 # default: reward of 0.5 if not done/ 1 if win/ 0 if lost
if done:
if reward == 1: # Won
reward = 1
elif reward == 0: # Lost
reward = -1
else: # Draw
reward = 0
if state.board[action]!=0: # invalid move: hard penalization
reward = -10
agent.memorize(np.array([state.board]), action, reward, np.array([next_state.board]), done)
# make next_state the new current state for the next frame.
state = next_state
total_rewards += reward
if len(agent.memory) > batch_size:
agent.replay(batch_size)
all_total_rewards[e] = total_rewards
avg_reward = all_total_rewards[max(0, e - 100):e].mean()
all_avg_rewards[e] = avg_reward
if e % 100 == 0 :
agent.save("./connectX-weights_deep.h5")
print("episode: {}/{}, epsilon: {:.2f}, average: {:.2f}".format(e, episodes, agent.epsilon, avg_reward))
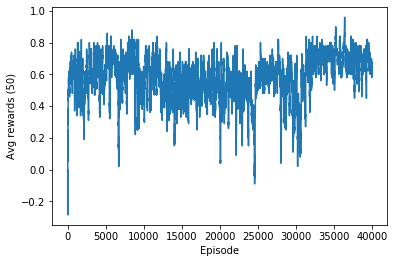
After a lot of training (millions of iterations with a prescheduled decreasing learning rate), the agent seems to have learned quite a bit: although I do not prevent the agent from choosing invalid actions, after some time such events basically do not happen anymore. Further, the agent starts winning against the random opponent with a fast increasing frequency.
episode: 39100/40000, epsilon: 0.01, average: 0.66
Invalid Action: Invalid column: 1
episode: 39200/40000, epsilon: 0.01, average: 0.65
episode: 39300/40000, epsilon: 0.01, average: 0.64
episode: 39400/40000, epsilon: 0.01, average: 0.78
episode: 39500/40000, epsilon: 0.01, average: 0.70
episode: 39600/40000, epsilon: 0.01, average: 0.68
episode: 39700/40000, epsilon: 0.01, average: 0.72
episode: 39800/40000, epsilon: 0.01, average: 0.68
episode: 39900/40000, epsilon: 0.01, average: 0.64
Did the agent learn anything?
The learned weights are used to compute actions of the agent during the games. The figure below shows the average rewards gained by the trained agent (including the penalty for chosing invalid actions).
import matplotlib.pyplot as plt
plt.plot(all_avg_rewards)
plt.xlabel('Episode')
plt.ylabel('Avg rewards (100)')
plt.show()
Finally, the real-life test: Submission of the agent to Kaggle. The procedure is somewhat cumbersome procedure because Kaggle does not allow keras modules for submission but the below procedure seems to work
model = Sequential()
model = Sequential()
model.add(Dense(20, input_dim=state_size, activation='relu'))
model.add(Dense(50, activation='relu'))
model.add(Dense(action_size, activation='linear'))
model.load_weights('connectX-weights_deep.h5')
layers = []
# Get all layers' weights
for i in range(3):
weights, biases = model.layers[i].get_weights()
layers.extend([weights, biases])
fc_layers = list(map(
lambda x: str(list(np.round(x, 8))) \
.replace('array(', '').replace(')', '') \
.replace(' ', '') \
.replace('\n', '') \
.replace(',dtype=float32',''),
layers
))
fc_layers = np.reshape(fc_layers, (-1, 2))
# Create the agent
my_agent = '''def my_agent(observation, configuration):
import numpy as np
'''
# Write hidden layers
for i, (w, b) in enumerate(fc_layers[:-1]):
my_agent += ' hl{}_w = np.array({}, dtype=np.float32)\n'.format(i+1, w)
my_agent += ' hl{}_b = np.array({}, dtype=np.float32)\n'.format(i+1, b)
my_agent += ' ol_w = np.array({}, dtype=np.float32)\n'.format(fc_layers[-1][0])
my_agent += ' ol_b = np.array({}, dtype=np.float32)\n'.format(fc_layers[-1][1])
my_agent += '''
state = observation.board[:]
# state.append(observation.mark)
out = np.array(state, dtype=np.float32)
'''
for i in range(len(fc_layers[:-1])):
my_agent += ' out = np.matmul(out, hl{0}_w) + hl{0}_b\n'.format(i+1)
my_agent += ' out = 1/(1 + np.exp(-out))\n' # Sigmoid function
my_agent += ' out = np.matmul(out, ol_w) + ol_b\n'
my_agent += '''
for i in range(configuration.columns):
if observation.board[i] != 0:
out[i] = -1e7
return int(np.argmax(out))
'''
with open('submission.py', 'w') as f:
f.write(my_agent)
Yes, she did!
from submission import my_agent
env = make("connectx", debug=True)
env.run([my_agent, my_agent])
print("Success!" if env.state[0].status == env.state[1].status == "DONE" else "Failed...")
def mean_reward(rewards):
return sum(r[0] for r in rewards) / sum(r[0] + r[1] for r in rewards)
# Run multiple episodes to estimate agent's performance.
print("My Agent vs. Random Agent:", mean_reward(evaluate("connectx", [my_agent, "random"], num_episodes=50)))
print("Random Agent vs. My Agent:", mean_reward(evaluate("connectx", ["random", my_agent], num_episodes=50)))
#print("My Agent vs. Negamax Agent:", mean_reward(evaluate("connectx", [my_agent, "negamax"], num_episodes=10)))
#print("Negamax Agent vs. My Agent:", mean_reward(evaluate("connectx", ["negamax", my_agent], num_episodes=10)))
So it seems that Deep-Q-Learning helped: by just playing against an random agent, the neural network was trained to win the game - even without knowing the rules in advance!
My Agent vs. Random Agent: 0.88
Random Agent vs. My Agent: 0.24